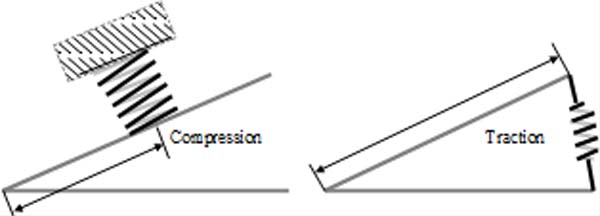
Obtenir une pression constante dans les réserves à soufflet
L'article précédent montre comment calculer la pression que donnera une réserve à soufflet, selon ses dimensions de volet, d'éclisses, etc.
L'intérêt est bien sûr d'aboutir à ce que cette réserve fournisse une pression constante pendant toute l'étendue de son fonctionnement, c'est à dire quelle que soit la position du volet.
Le moyen d'y parvenir est, connaissant le couple généré par une pression constante dans cette réserve, de fournir un couple opposé égal à tout instant à celui-ci. Ce dernier couple, dans nos orgues de barbarie, est généré par un ressort. On calcule le couple en multipliant la force du ressort (pour l'élongation concernée) par la distance de son point d'application à l'articulation du volet.
Calcul à la conception de la réserve (cas de réserve en pression).
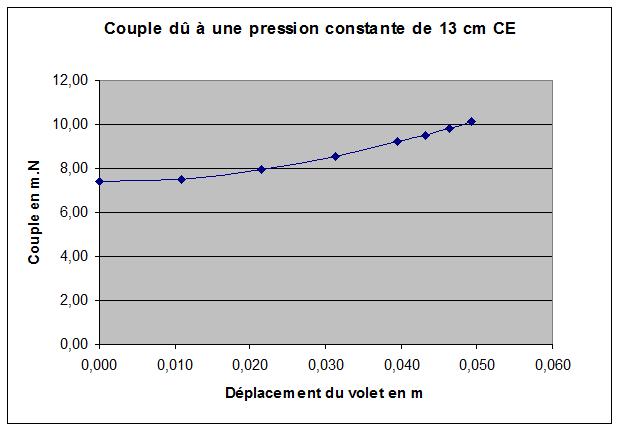
On a calculé le couple généré par la pression désirée, avec les caractéristiques de la réserve en projet. Soit, avec les données de mon BB29, et une pression de 13 cm CE:
Le diagramme force / élongation d'un ressort étant représenté par une droite, il sera judicieux pour le déterminer de partir des valeurs calculées ci-dessus.
Pour l'exemple considéré, en traçant une droite au plus près du couple calculé:
Pour d = 0, , la droite passe à 7 N.m environ.
Force du ressort nécessaire = couple divisé par le bras de levier = 7 / 0.36 m = 19.4 N
Pour d = 5, , la droite passe à 10.4 N.m environ.
Force du ressort nécessaire = couple divisé par le bras de levier = 10.4 / 0.36 m = 28.9 N
Raideur: (28.9 - 19.4) / 5 cm de débattement = 1.9 N/cm
Munis de ces renseignements, il convient de consulter sur internet le site d'un fabricant de ressorts: par exemple le site de la Société VANEL.
Et faire une "recherche avancée" dans les ressorts de traction ou de compression, où on pourra utiliser les données ci-dessus.
Attention: il faut se souvenir que deux ressorts identiques mis en parallèle (pour augmenter la force résultante par exemple) voient leurs raideurs s'ajouter.
Calcul simplifié pour une réserve existante (cas de réserve en pression).
Je vous propose ici une méthode pour améliorer vos réserves à soufflet déjà construites, moyennant quelques mesures et quelques calculs faciles.
Le principe de base est de comprendre que la pression interne est due à la force avec laquelle le ressort appuie sur le volet mobile, sachant que cette pression interne génère elle aussi des forces relativement complexes.
Couples engendrés
Ces forces agissent selon la distance de leur point d’application avec le point d’articulation du volet (bras de levier). Les couples sont le produit de ces valeurs.
Couple = force x bras de levier
1 / Les forces dues à la pression interne sur les éclisses et le volet mobile varient en fonction de la pression bien sûr, et de la position haute ou basse du volet, donc de l'inclinaison des éclisses. Le bras de levier est considéré comme indéterminé.
2 / La force générée par le ressort varie en fonction de l'élongation (ressort de traction) ou le raccourcissement (ressort de compression) de ce ressort. Le bras de levier est la distance entre le point d’articulation du volet et le point de tire (ou de pression) du ressort.
Si ce couple « ressort » est à tout instant égal – et opposé - au couple « pression » évoqué plus haut, la pression interne restera constante pendant toute la phase d’utilisation de la réserve.
Je vous propose de chiffrer ces valeurs, facilement, en suivant les méthodes A, B, et C ci après.
On pourra ainsi déterminer la force nécessaire à demander au ressort, et la raideur de celui-ci, pour atteindre le but recherché. (Raideur : c’est la variation de force du ressort par rapport à la variation de longueur concomitante).
A Mesure des caractéristiques du ressort utilisé.
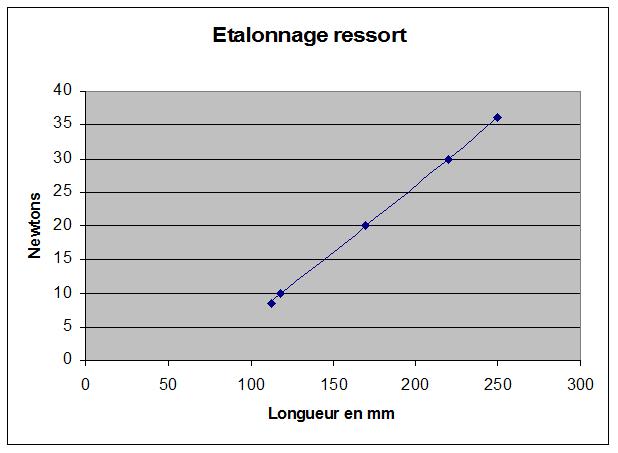
Il est nécessaire de réaliser un « étalonnage » du ressort, c'est à dire un diagramme force / longueur.
Pour les unités, il est préférable pour ne pas s'emmêler de noter les forces en Newtons (on peut adopter 1 Kg = 10 N. ; si on voulait être très rigoureux, il faudrait prendre 1 Kg = 9,81 N, mais ce n'est pas utile dans le cas présent).
Méthodes :
Pour un ressort de traction, il suffit d'accrocher le ressort à une potence, de suspendre des poids à l'autre extrémité, et de mesurer la longueur du ressort résultante. (Ne pas inclure les boucles dans cette mesure).
Pour un ressort de compression, il faudra peut-être réaliser un bâti pour éviter que le ressort ne « flambe ». Une planchette avec charnière peut convenir. Attention dans ce cas à minimiser ou tenir compte des effets de levier éventuels qui risquent de perturber la mesure. Il faut mettre les poids bien en face de l'appui du ressort. Il faut se débrouiller aussi pour que l'axe du ressort reste vertical, ou plutôt que le poids agisse bien verticalement à chaque mesure, pour que la force relevée soit bien celle dudit poids, et pas son cosinus.
Nous aurons deux séries de chiffres par ressort, à partir desquels nous pourrons construire les diagrammes.
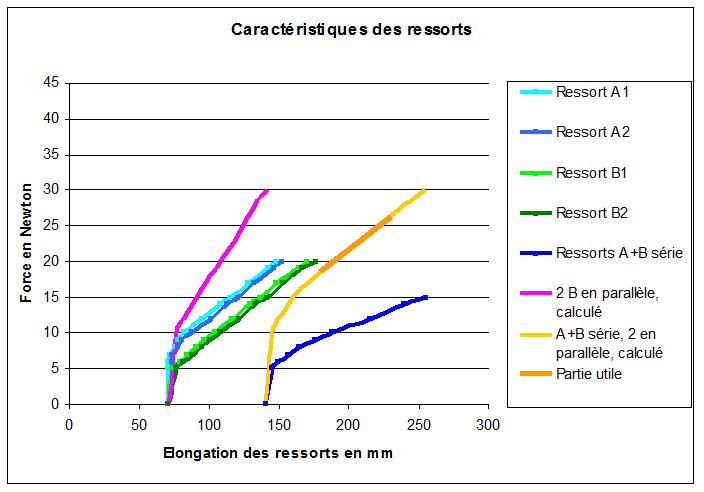
Pour illustrer le propos, voici les valeurs obtenues avec le matériel (ressorts de traction) dont je dispose :
B Mesure de la courbe : pression délivrée en fonction du déplacement du volet mobile.
Méthode :
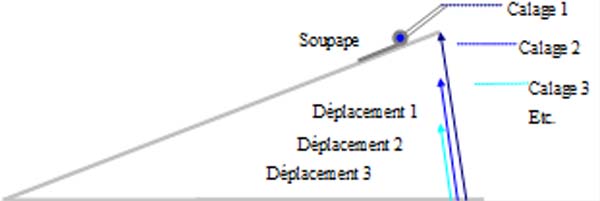
Tout étant en place pour le fonctionnement normal de la soufflerie, ajuster le niveau de la butée de la soupape de décharge à différentes valeurs, pour obtenir différentes positions du volet mobile.
Noter les valeurs de pressions obtenues au pèse-vent, et les positions de volet mobile correspondantes. ( On peut brancher le pèse-vent sur une embase de flûte retirée, et scotcher la flûte de Pan en laissant libre cette note )
Construire soigneusement un diagramme des valeurs obtenues.
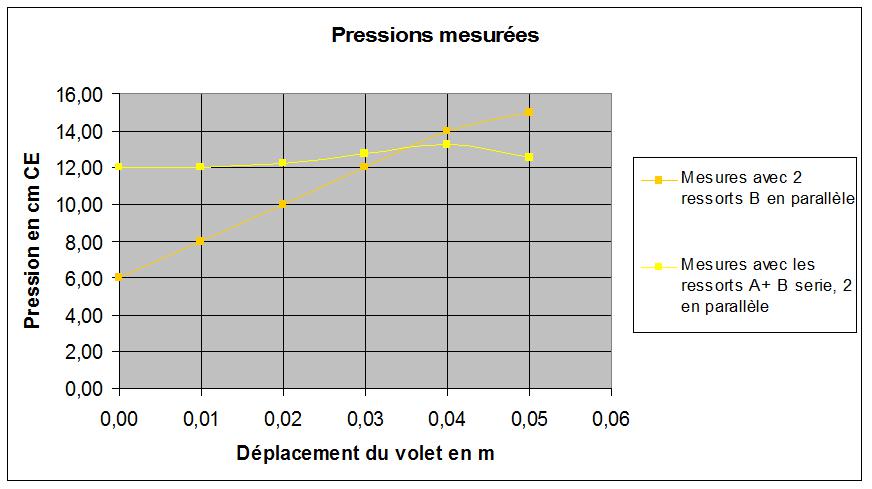
Exemple : Valeurs obtenues avec la combinaison de ressorts
Au passage, avec ces ressorts non optimisés, on observe a priori une pression différente pour chaque position du volet mobile, ce qui pourrait être utilisé pour régler la pression de fonctionnement, si on n'allait pas jusqu’au bout de la présente démarche. (C'est ce que j'ai fait sur mon mini 29).
C Mesure du bras de levier d'action du ressort.
C'est la distance entre le point d'application de la force du ressort, et l'articulation du volet mobile.
Pour ne pas s'emmêler, il est préférable de l'exprimer en mètres.
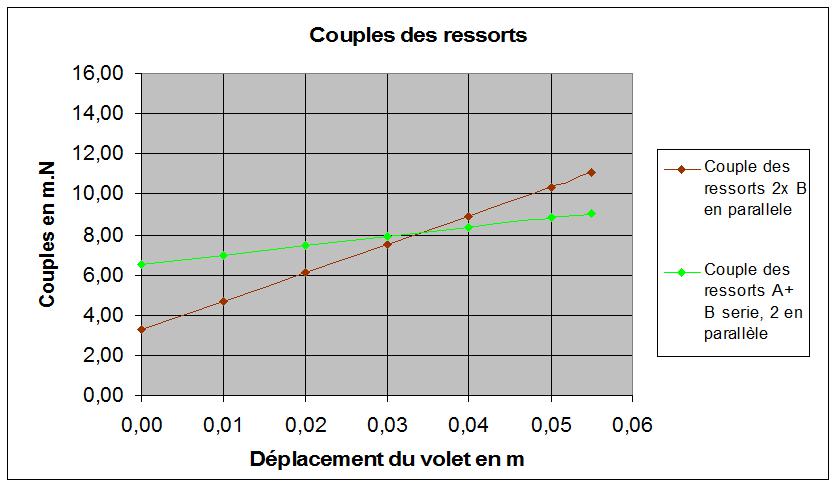
Nous pouvons construire avec soin un diagramme : couple du ressort en fonction du débattement du volet mobile.
Le couple est le produit force du ressort x bras de levier, pour chaque débattement du volet mobile et donc chaque longueur du ressort.
Dans mon exemple, le bras de levier est de 0,36 m.
D Calcul des caractéristiques de la réserve en essai.
Nous allons calculer des « coefficients » caractérisant la réserve en essai, qui, étant le résultat de mesures réelles, incluent l'effet des éclisses quelles que soient leurs formes.
Il suffit pour chaque position du volet, de diviser le couple ressort correspondant, par la pression mesurée dans cette position. Ces valeurs sont tirées des diagrammes construits ci-dessus
En fait, les variations étant linéaires (ou quasi), il suffit de faire ce calcul pour les positions hautes et basses du volet mobile.
Nommons ces résultats Coeff.(maxi) et Coeff.(mini) pour respectivement les positions haute et basses du volet mobile.
Exemples avec mon matériel :
Ressorts A+B série, deux en parallèle
Coeff.(maxi) = 9,05 N.m / 12,5 cm CE = 0,724
Coeff.(mini) = 6,48 N.m / 112 cm CE = 0,540
Deux ressorts B, en parallèle
Coeff.(maxi) = 11,06 N.m / 15 cm CE = 0,737
Coeff.(mini) = 3,24 N.m / 6 cm CE = 0,540
On pourra adopter : Coeff.(maxi) = 0,73 et Coeff.(mini) = 0,54 , pour caractériser ce matériel.
E Calcul du ressort optimum.
A ce stade, nous sommes maîtres de décider de la pression de fonctionnement souhaitée.
Dans ces conditions, les forces à demander au ressort sont :
Force maxi. = Coeff.(maxi) x Pression / Bras de levier ressort
Force mini. = Coeff.(mini) x Pression / Bras de levier ressort
Et la raideur à exiger est :
(Force maxi - Force mini ) / Variation de longueur correspondante
Soit pour l'exemple considéré et le choix de 13 cm CE:
Pour d = 0 , force minimale :
0,54 x 13 / 0,36 = 19,5 N
Pour d = 5 , force maximale :
0,73 x 13 / 0,36 = 26,4 N
Raideur ( 26,9 N - 19,5 N ) / 5 cm de débattement réel = 1,38 N/cm
Munis de ces renseignements il convient de consulter sur internet le site d’un fabricant de ressorts : le site de la société Vanel convient bien : www.vanel.com/index.php?lang=french
Et faire une « recherche avancée » dans les ressorts de traction ou de compression où on pourra utiliser les données ci-dessus.
Vous y trouverez même des indications (diamètre de la corde à piano, diamètre du ressort, nombre de spires, etc) si vous voulez tenter de bricoler vos ressorts vous même, sans garantie du résultat !. C'est à mon avis une option plus chère que de commander le bon ressort.
Attention : il faut se souvenir que deux ressorts identiques mis en parallèle (pour augmenter la force résultante) voient leurs raideurs s’ajouter : pour 1,38 N/cm calculés, il faudra pour deux ressorts en parallèle demander 0,69 N/cm à chacun.
Pour mon exemple, je trouve qu'avec deux éléments en parallèle (configuration de ma soufflerie oblige), la référence U. 111.070.0450.AX conviendrait.
Pour le moment, je garde mon montage d'essai, qui n'introduit que 1 cm CE de variation de pression, ce qui est négligeable au vu des autres paramètres, notamment des pertes de charge du système, que l'on va étudier dans un autre article.
Vue des ressorts d'essai en série.
Le même montage est installé symétriquement de l'autre coté des soufflets
Calcul pour une réserve en dépression (certains orgues à anches).
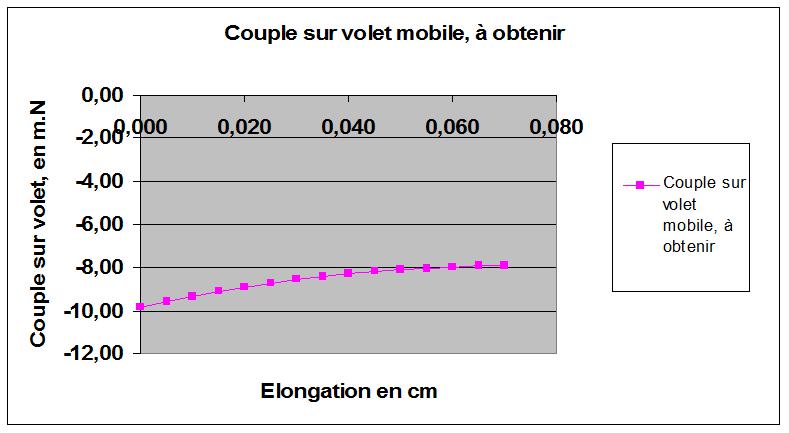
A l'aide des calculs de l'article « Une réserve à soufflet mise en chiffres », on peut définir le couple à exercer sur le volet mobile, et ses variations, pour obtenir une dépression constante dans la réserve d'un OdB à anches fonctionnant en dépression.
Ce calcul tient compte des forces exercées par la pression sur le volet mobile et sur les éclisses.
On se rend compte que pour avoir cette dépression constante de -10 cm CE, il faut exercer un couple de -9,84 m.N à la position « 0 » -repos- du volet, jusqu'à -7,93 m.N à la position maxi du volet (70 mm), correspondant à la tension maximum du ressort.
Le couple à exercer est donc moindre en position tendue du ressort qu'en position repos !
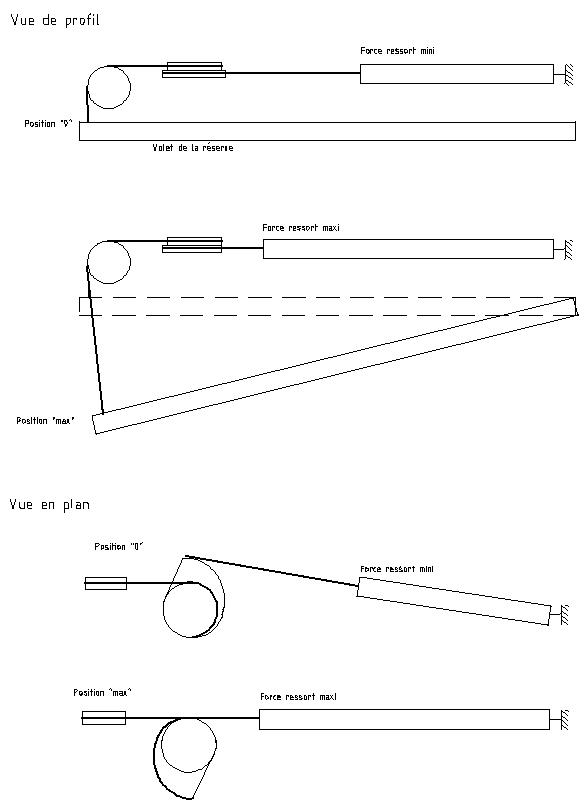
Pour obtenir ce résultat paradoxal, il faut recourir à un adaptateur conçu de la manière suivante
1 - Une poulie circulaire munie d'une gorge permet d'exercer sur le volet mobile - par l'intermédiaire d'un câble - une force mécanique ad hoc générant le couple calculé plus haut.
Le déplacement du volet mobile doit correspondre exactement à la rotation de cette poulie.
Des essais préalables ont montré qu'une rotation de ¾ de tour convient bien.
Définition de la poulie :
La circonférence est de 2 * Π * R.
¾ de circonférence font : ( 3 / 4) * 2 * Π * R = ( 3 / 2 ) * Π * R
Pour un course de volet de 70 mm, R = 70 * ( 2 / 3 ) * Π
= 14,85 mm
Soit un diamètre de la gorge de 29,7 mm
2 - Le couple à exercer est fourni par la force d'un ressort de traction, dont le point d'application va varier en fonction de la rotation d'une poulie spirale solidaire de la poulie ronde ci-avant. Le rayon de cette poulie spirale est calculé pour que le couple résultant (sur les poulies) soit celui souhaité.
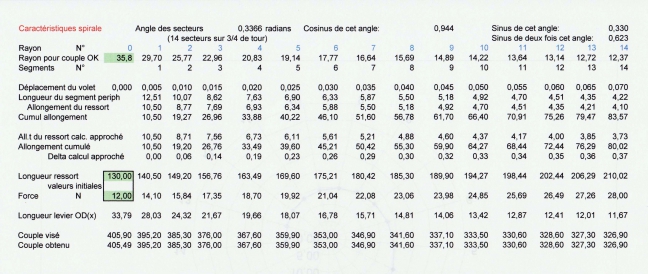
Tableau Excel de calcul du couple sur les poulies :
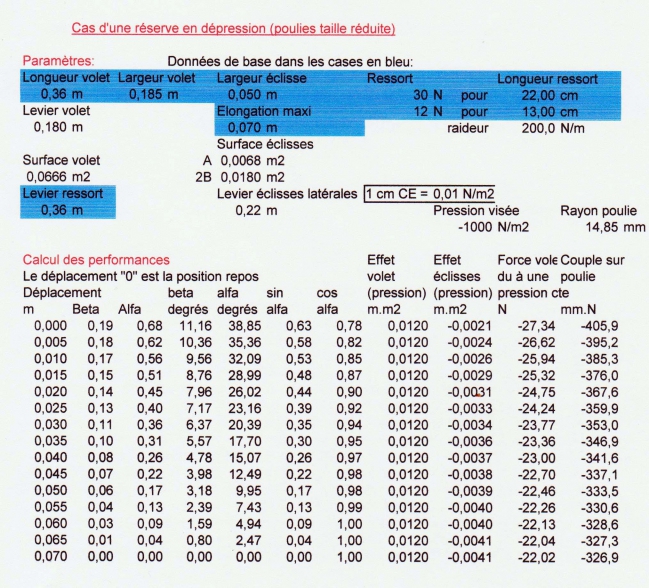
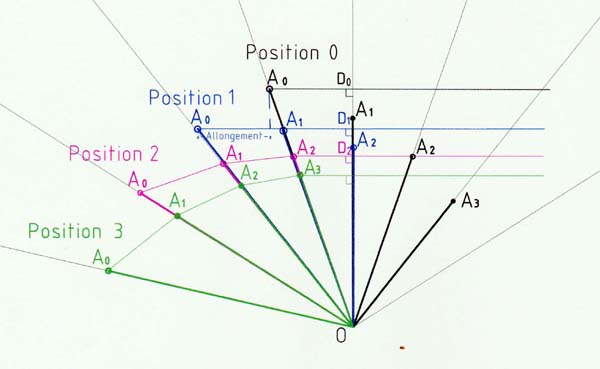
Voir le principe de fonctionnement du dispositif ci après.
Quand on regarde ce dispositif, on s’aperçoit que l'allongement du ressort est exactement égal à la longueur développée de la périphérie de la spirale. Pour connaître la force exercée par le ressort, il faut connaître :
- Les caractéristiques force/allongement du ressort envisagé.
- La longueur développée de la circonférence de la poulie.
A Déterminer les caractéristiques Force / Élongation d'un ressort de traction
Il est nécessaire de réaliser un « étalonnage » du ressort, c'est à dire un diagramme force / longueur.
Pour les unités, il est préférable pour ne pas s'emmêler de noter les forces en Newtons (on peut adopter 1 Kg = 10 N. ; si on voulait être très rigoureux, il faudrait prendre 1 Kg = 9,81 N, mais ce n'est pas utile dans le cas présent).
Méthode :
Il suffit d'accrocher le ressort à une potence, de suspendre des poids à l'autre extrémité, et de mesurer la longueur du ressort résultante.(Ne pas inclure les boucles dans cette mesure).
Nous aurons deux séries de chiffres par ressort, à partir desquels nous pourrons construire les diagrammes.
Pour illustrer le propos, voici les valeurs obtenues avec le matériel (ressort de traction) dont je dispose :
B Déterminer la longueur utile développée sur la poulie spirale
Les deux poulies circulaire et spirale sont solidaires, et nous avons choisi (après expérimentation) une rotation de ¾ de tour représentant 70 mm de course du volet. Nous divisons cette course en 14 éléments, pour voir une valeur chaque 0,5 cm (7,0 cm / 14 ) . On aura ainsi 14 couples à définir.
On constate, après un premier calcul, que quand la poulie spirale tourne, que le câble relié au ressort ne peut pas rester tangent au contact de celle-ci . La distance à l'axe n'est pas le rayon de la spirale, et par conséquent, le couple calculé s'en trouve faussé.
Il faut donc créer une autre spirale dont les rayons sont tels que la distance à l'axe du câble du ressort permettent de respecter les couples calculés. Ces distances à l'axe sont en fait les rayons de la spirale calculée initialement. On observe que en avançant la deuxième spirale en calcul d'un secteur de 19°3, cela amène le câble sur le rayon calculé suivant de la spirale initiale. Ce décalage est donc une solution au problème.
Mais cette solution va modifier les valeurs d'élongation du ressort, l'allongement n'est plus exactement égal à la périphérie de la spirale, il faut donc tout recalculer.
Rotation de la spirale et calculs d'allongement du ressort
De la position 0 à la position 1
L'allongement est : A0D1 – A0D0
soit OA0* sin 2 ɤ - OA0*sin ɤ
Autre façon de calculer :
L'allongement est donné par : le premier élément de la périphérie de la spirale A0A1, plus la distance de l'extrémité la plus proche à l'axe vertical A1D1, moins la longueur A0D0 mobilisée initialement ;
(A0A1 + A1D1) – A0D0
soit A0A1 + OA1* sin ɤ - OA0*sin ɤ
A0A1 est calculé par la formule de résolution d'un triangle :
le troisième côté = racine carrée de (a²+ b² – 2.a.b.cos ɤ)
avec a et b = rayons de la spirale
ɤ = angle au sommet du triangle = 19°3
L'allongement devient (a²+ b² – 2.a.b.cos ɤ)^0,5 + OA1 * sin ɤ - OA0*sin ɤ
De la position 1 à la position 2
(A0A1 + A1A2 + A2D2) – A1D1
De la position 2 à la position 3
(A0A1 + A1A2 + A2A3 + A2D2) – A2D2
Et ainsi de suite...
Ces allongements successifs de ressort permettent de calculer à chaque position les forces exercées par le ressort.
Force ressort = k . x + b
avec (déterminés sur le diagramme d'étalonnage du ressort)
k =raideur du ressort k pour le ressort utilisé : 10 N / 5 cm soit 2 N/cm ou 0.2 N/mm
x = augmentation d'élongation
b = force à l'origine
Sur ces bases, connaissant le couple nécessaire, on peut calculer le rayon à donner à la spirale à chaque position :
Le couple souhaité est celui calculé pour cette position (x).
La distance de la direction de traction, à l'axe de rotation des poulies est :
OD(x) = Couple(x) / force ressort (x)
Le rayon de la spirale est :
OA(x) = OD(x) / cos ɤ = Couple(x) / ( force ressort (x) * cos ɤ )
L'inconvénient de cette méthode exacte, est de faire intervenir des points ( A1 , A2 , A3 ) que l'on n'a pas encore calculés dans le processus de calcul automatique Excel, et donc de bloquer dans ce calcul.
Je propose donc ci-après un autre calcul qui n'a pas ce défaut, mais qui a celui d'être seulement approché. On aura donc ensuite le choix : soit de se contenter du calcul automatique, mais approché, soit de reporter manuellement dans le tableau Excel les valeurs exactes calculées sur ces bases, une par une, avec un recalcul à la clef . Cependant, les écarts sont minimes, et de l'ordre de la précision de fabrication manuelle.
Calcul d'allongement approché, mais automatique
De la position 0 à la position 1
L'allongement est : A0D1 – A0D0
soit OA0* sin 2 ɤ - OA0*sin ɤ =
De la position 1 à la position 2
Allongement = environ A1D2 - A1D1
soit OA1* sin 2 ɤ - OA1*sin ɤ
De la position 2 à la position 3
Allongement = environ A2D3 - A2D2
soit OA2* sin 2 ɤ - OA2*sin ɤ
Tableau Excel de détermination des dimensions de la spirale.
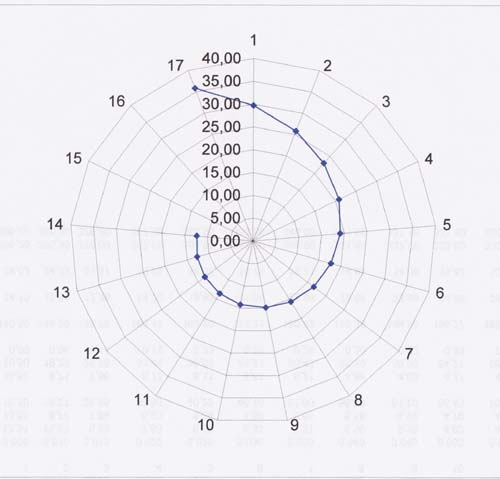
Allure de la spirale :
Ces résultats de calculs sont en cours d'expérimentation pour en vérifier la validité; mais cela peut prendre quelque temps ...
A suivre....
Eh bien, après réalisation du système et essais, cela marche et cela ne marche pas !!!!
Je suis parvenu à faire une spirale qui fournit une dépression approximativement constante, quand on appuie sur le volet et qu'on laisse le ressort le faire revenir seul. Mais ce ne fut pas sans mal, la réalisation manuelle de la spirale manque de précision, et les frottements des différents renvois amènent beaucoup de perturbations.
Mais quand on en vient au fonctionnement normal, avec alimentation par le soufflet et la manivelle, la régulation qui devrait s'exercer est insuffisante, et la dépression n'est pas constante , et de loin...
Une réflexion sur la géométrie de l'ensemble de la soufflerie me semble nécessaire. Comme disait Boris Vian (La Java de la bombe atomique) : Y a que'que chose qui cloche la-dedans, j'y retourne immédiatement...
A suivre à nouveau.....
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 21 autres membres